玉手箱の計数では、計算問題と図表問題のどちらかが出題されます。
まずは計数の基本形式を確認し、それぞれの問題の解き方を確認していきましょう。
例題や問題別の対策ポイントも解説しているので、勉強を始める際はぜひ参考にしてください。
目次
玉手箱の計数はどんな問題が出る?
計算か図表問題だけの出題
| 四則逆算 | ・ 等式の空欄に当てはまる数値を答える ・ 9分で50問 |
| 図表の読み取り | ・ 図表を見て問いに答える ・ 15分で29問または35分で40問 |
| 表の空欄推測 | ・ 図表の空欄に当てはまる数値を推測する ・ 20分で20問または35分で35問 |
玉手箱の計数は、計算力を問われる「四則逆算」と、図表を読み取って答える「図表の読み取り」「表の空欄推測」に分けられます。この中から1つだけが出題され、最後まで同じ種類の問題を解いていきます。
「四則逆算」では、1~3桁程度の数字を使った等式に、1つだけ空欄がある問題が出題されます。空欄に当てはまる数値は、式を変形して求めるのが基本です。難しい計算は求められないので、カッコがある時の計算順や、移項などの知識があれば解けない問題はないでしょう。
ただし、時間内に解き終えるためには素早い計算が必須です。1問あたり10~15秒程度しかかけられないため、急いで計算しないとすぐに時間切れになってしまいます。
また、図表問題の「図表の読み取り」 「表の空欄推測」は、どちらも図表を読み取って答える問題です。どちらも最低限の計算は必要ですが、それよりも効率的に読み取りをできるかが重要になります。
「図表の読み取り」では、図表の特定の項目に着目して、他の数値と比べた時の「合計・差・割合・変化率」などを求めます。計算は簡単ですが、公式がわからないと時間がかかるものが多いです。
一方、「表の空欄推測」は図表の中にある空欄に入る数値を推測して答えます。計数問題の中では唯一「はっきりとした答えが出ない問題」のため、苦戦しやすい分野です。
効率良く解くためには、他の項目との比例・反比例といった関係を素早く見つけて、大まかな数値を割り出す必要があります。正確に計算できなくても答えを出せるため、解答パターンを理解してしまえば余裕を持たせやすい問題です。
全て5択の選択式問題
玉手箱の計数問題は、どれも5択の選択式です。答えを正確に記述する必要がないため、計算結果が少し間違っていても正解できる可能性があります。
5分の1が正解となるため、当てずっぽうで選んでも20%程度の正答率が期待できます。大まかに計算してみて数値の目安がわかれば、さらに「消去法」で絞り込むことも可能です。
ただし、選択肢は計算ミスを見据えた数値に設定されていることも多く、全部を概算だけで答えるのは危険です。本番ではメモ用紙も使用できるため、途中式や計算結果をメモして正確な答えを出しておくことが重要になります。
電卓前提の計算もある
Webテスト形式の玉手箱では、電卓を使うことが可能です。そのため、明らかに暗算や筆算で解くことを前提としていない計算量の問題も出題される傾向にあります。
4桁以上の整数や、小数第3位以下まであるような小さな数などもあり、電卓を使わないと手間がかかります。自力で解くこともできますが、制限時間内に解き終えることは難しいでしょう。
一見すると暗算でも解けそうな問題が、実は電卓を使った方が早いというケースもあります。暗算・筆算・電卓の使い分けを瞬時に判断することが必要です。

計数問題の解き方は3パターン
四則逆算
| 問題形式 | 解き方 |
| ・ 1つだけ空欄がある等式 ・ 空欄に入る数値を選ぶ ・ 整数以外に分数・小数も出る |
・ 移項などで式を整理するのが基本 ・分数は通分や約分が必須 ・ 小数は桁に注意する |
四則逆算では複雑な式は出てこないので、空欄を片方の辺に残すように式を整理するだけで解くことができます。計算自体も、基本的な四則演算だけできれば十分です。
頻出の解き方は、「辺が空欄だけになるように移項」「空欄の係数を消すように両辺を割る」の2つです。
例えば、「 【 】+A=B-C」の場合は、「+A」の部分を右辺に移項して「 【 】=B-C-A」にすることで計算できます。この時、必ず正負の符号を反転させることを忘れないようにしましょう。
また、「A×【 】=B+C」のような式では、空欄に掛けてあるAで両辺を割る必要があります。
ただ割っただけだと「 【 】=B÷A+C÷A」と少しわかりにくい式になるため、「 【 】=(B+C)÷A」のようにカッコを活用すると効果的です。
使われる計算は四則演算のみであり、指数や√などは出題されません。数学に苦手意識がある人でも、特に問題なくこなせる計算内容です。
図表の読み取り
| 問題形式 | 解き方 |
| ・ 様々な形式の図表が提示される ・ 特定の項目の「合計、差、割合、変化率」などを求める ・ 解答に関係ない数値が多い |
・先に問題文を見る ・ 解答に関連する項目だけ読み取る ・割合と変化率の計算方法に注意する ・ 数値が多い時は必ずメモする |
図表の読み取りは、図表よりも先に問題文を見ておくことが重要な単元です。解答に必要なのは1~2個程度の数値なので、他の数値を見る必要がありません。
問題文から「何を計算すればいいのか」を確認しておけば、関係ない項目には目を通さずに済みます。
図表は毎回ランダムな形式で、テーマや数値も様々です。形式ごとに軸や単位の見方などを押さえておくと、スムーズに解答できます。
問われるものとしては、「合計・差・割合・変化率」の4つが頻繁に出題されます。例えば、「〇年から×年でいくつ増加したか」という問題文の場合は、差を求める問題だとわかります。
また、頻出パターンを複合した問題が出ることもあります。「A、B、Cの合計は、〇年から×年で何%増えたか」といった内容では、合計を計算してから変化率を求めることが必要です。
こうして計算の段階が増えるほど、覚えていなければならない数値は増えます。簡単な数値であってもメモ用紙に書き、忘れないようにしておきましょう。他の数値を意識しながら計算をするのはミスの原因になるため、解いている数字に集中しましょう。

表の空欄推測
| 問題形式 | 解き方 |
| ・1つだけ空欄が含まれる図表が提示される ・ 空欄に入る数値を「推測」する ・ 正確な数値は求められないことが多い |
・空欄を含む列や行の規則性を探す ・ 他の項目との関連性を見つける ・ 概算でも解けることがある |
表の空欄推測では、空欄以外の数値から規則性を見つけることが解答のカギになります。図表の各項目には関連があるはずなので、全ての数値がヒントといえます。
例えば、「売上」の列に空欄があり、その他に「来客数」といった項目があれば、売上と比例関係にあることが推測できます。その上で、「来客数が多い時は売上も多いか」 「片方が増えるともう片方はどの程度増えるか」を確認してみましょう。
規則性が明らかになったら、空欄に入る数値を計算することができます。ここでは明確な数字が出ないことも多く、最終的には推測に最も近い数値を選ぶことになります。
空欄に当てはまる数値に近いものを選べばいいので、小数点以下まで正確に計算する必要はありません。計数の中では唯一、概算でも正解しやすい問題といえます
また、はっきりとした規則性が見えていなくても、「明らかに違う」という数値を除くことはできます。2~3択まで絞り込めれば、最後は適当に選んでも正答できる確率が高いです。
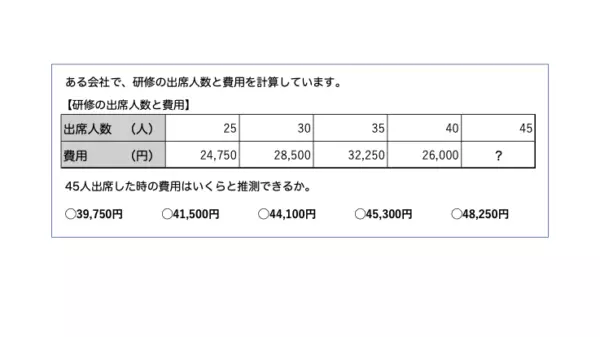
【例題を見る】玉手箱の計数問題
四則逆算の例題
【 】に入る数値として正しいものを、選択肢の中から1つ選びなさい。
【選択肢】
A:
B:
C:
D:
E:
解答: A
・・・①
・・・②
・・・③
①左右の式を入れ替える(【 】が左辺にくる)
②17と27を右辺に移す(左辺の計算順が後の27が先)
③左から順に電卓で計算する
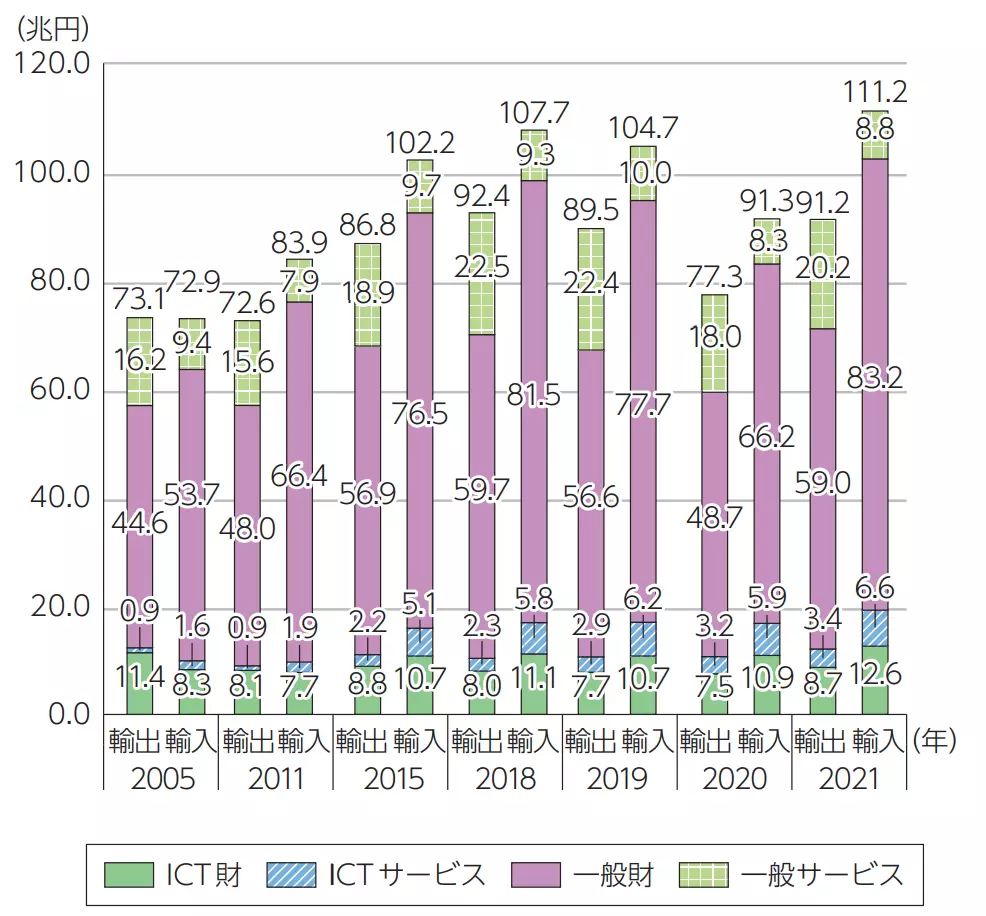
図表の読み取りの例題
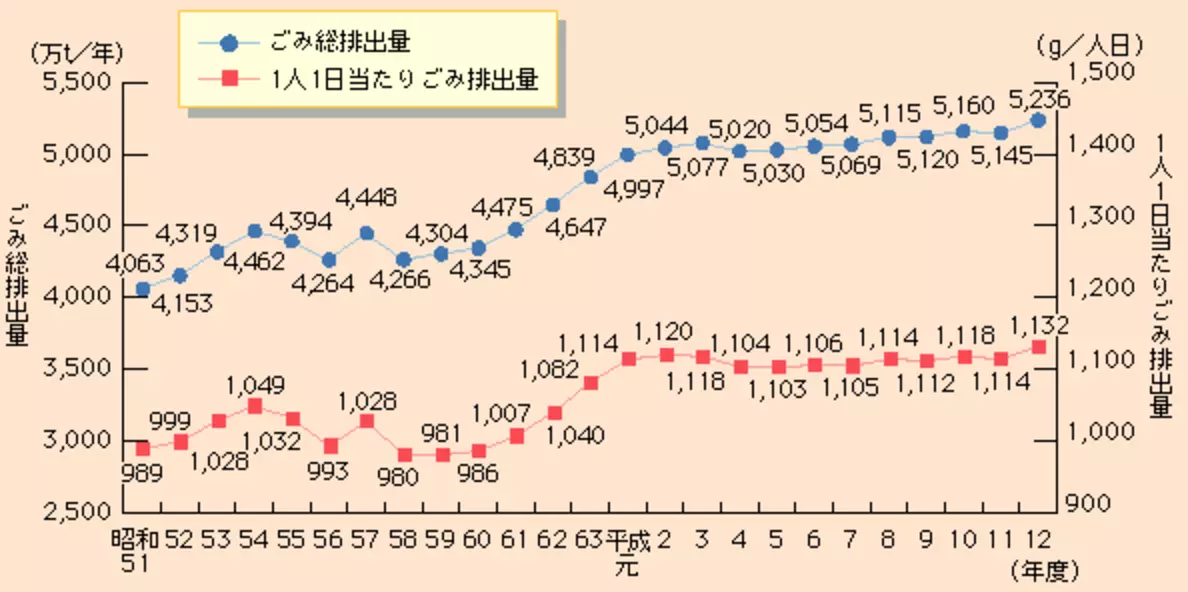
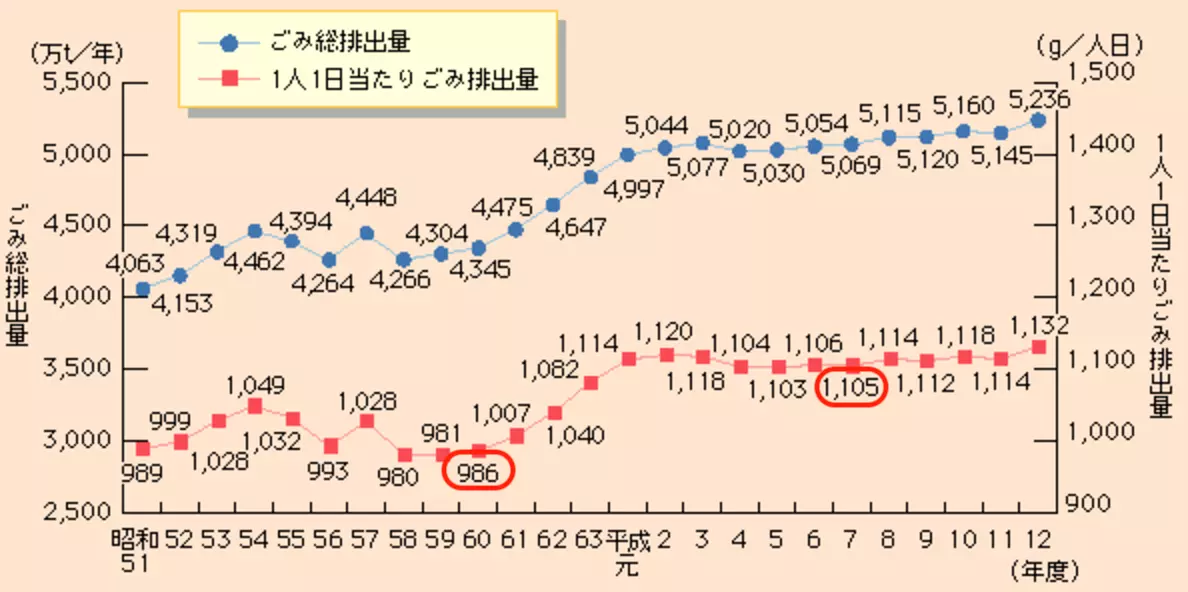
出典:平成15年版環境白書|環境省
平成7年度の1人1日当たりのごみ排出量は、昭和60年度の1人1日当たりのごみ排出量と比べておよそ何%増加したか。最も近いものを、以下の選択肢の中から1つ選びなさい。
【選択肢】
A: %
B: %
C: %
D: %
E: %
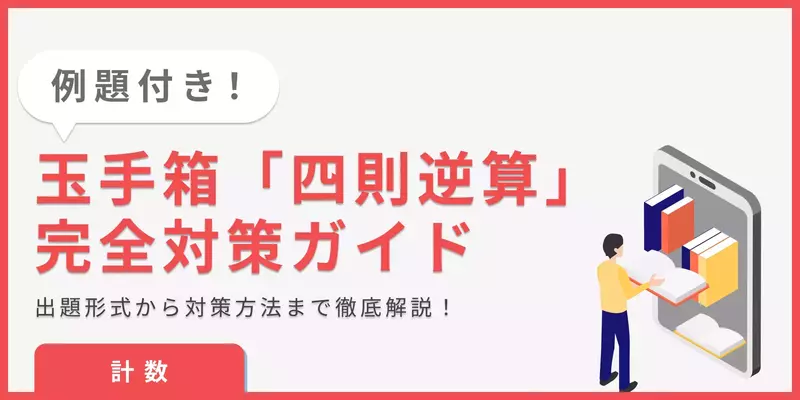
表の空欄推測の例題
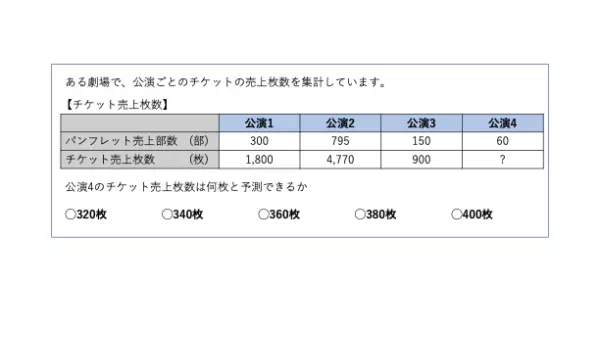

チケット売上枚数は、パンフレット売上部数に比例して増えている。
各公演の「チケット売上枚数÷パンフレット売上部数」を計算すると、いずれも6倍。
公演4のパンフレット売上部数を6倍すれば、チケット売上枚数が求められる。
解答:枚
計数対策は計算と図表問題に分けて進める!
【計算】分数・小数を正しく計算できるようにする
=
=
◆分数同士の掛け算
◆ 小数同士の掛け算
◆ 小数同士の割り算
分数と小数の計算方法は、問題を解く際、常に使用するため必須の知識です。日常ではあまり使わない知識のため、意外と忘れている人も多いでしょう。
分数では、「足し・引き」と「掛け・割り」でそれぞれ注意点が異なります。
分数を足したり引いたりする時には、まず両方の分母を揃える必要があります。この時、分母と分子の両方に同じ数字を掛けることを忘れてしまい、分母だけを増やしてしまうミスが多いため注意しましょう。
分数の掛け算では分子同士と分母同士を掛けます。割り算の場合は、割る方の分数の分子・分母を逆にしてから掛けることで計算できます。
一方、小数では「掛け・割り」の際の桁数が重要です。「小数第二位×小数第三位」のような計算の場合、0が何個も続くため間違えやすいです。
さらに、小数で割る時の正しい計算方法も必ず押さえておく必要があります。考え方はいくつかありますが、簡単なのは「分数に直す」という方法です。
例えば、「0.2」で割る時はわかりやすく「2/10」という分数に直しましょう。その後、通常の分数の割り算と同じく「分子と分母を逆に」してから掛けることで答えが求められます。
【計算】電卓の操作に慣れる
Webテスト形式の玉手箱では、電卓を使用できます。暗算で解ける問題もありますが、中には電卓を使った方が早い計算も出題されます。
「暗算と電卓どちらが早いか」を分けるのは、暗算力と電卓の操作速度です。暗算力を短期間で上げるのは現実的ではありませんが、電卓の操作に慣れるのは数日あれば可能でしょう。
「暗算で解けなくもない」という計算量の問題でも、電卓で素早く計算できた方が時短できます。時間制限が厳しい玉手箱では、こうした細かい時間の節約が積み重なって得点へ繋がります。
なお、本番で使えるのは電卓機能だけの機器となっています。普段はスマホやPCの電卓機能を使っている人でも、必ず実物の電卓を用意し、操作に慣れておくようにしましょう。

【図表】必要な公式を暗記する
倍
◆ 「AはBの何%か」
%
◆ 「AからBまで何%増えたか」
%
または
%
図表問題で頻出の「割合」 「変化率」の計算には、それぞれ公式が必要になります。その場で計算方法を考える時間はないので、事前に暗記しておくことが重要です。
割合は「比べる量÷もとの量」で求めることができます。この場合は「〇倍」という表記になり、%で答える場合はここに100を掛ければ求められます。
「比べる量」 「もとの量」という表記でわかりにくければ、「割合を求める量」 「基準となる量」と言い換えても良いでしょう。「AはBの何%か」という問いであれば、Aが「割合を求める量」、Bが「基準となる量」となります。
一方、変化率は「どれだけ増えたか(減ったか)」を求める計算をします。「変化前の量」が基準となり、「変化した量」がその何%なのかを計算すれば、変化率がわかります。
例えば、「AからBまでに何%増えたか」といった問題の場合は、Aが「変化前の量」にあたり、BからAを引いた数が「変化した量」です。
つまり、「B-A」を「A」で割って割合を出し、最後に100を掛けることで%として求められます。
また、「B÷A-1」に100を掛けるという簡単な計算方法もあります。ただし、こちらは変化前・変化後の関係をしっかり理解してから使うことをおすすめします。
これら3つの公式を暗記しておき、問題文で求められている計算を迷わずに行えるようにしましょう。
【図表】頻出の図表5種類を覚える
・ 棒グラフ
・ 折れ線グラフ
・ 帯グラフ
・ 円グラフ
図表問題では、主に5種類の図表が提示されます。どれも正しい読み取り方がわかっていないと致命的なミスに繋がるため、特徴を押さえておきましょう。
表は、項目が最上段だけに並んでいるものと、逆L字に並んでいるものがあります。逆L字の場合は、縦と横の項目を組み合わせて見る必要があり、「(縦の項目)年の(横の項目)人」という読み方になります。
また、棒グラフ・折れ線グラフ・帯グラフでは、縦と横の軸がそれぞれ何を表しているのかが重要です。特に、単位が「1万個」のようになっている場合は注意しましょう。グラフ上の数字に、単位となっている数を掛けたものが実数値となります。
円グラフは、グラフ外に単位や合計などを記載していることが多いため、グラフだけに注目しないようにしましょう。また、色や模様が何を示しているのかを必ず見比べながら読み取りする必要があります。
【図表】空欄推測の解答パターンを知る
・ 共通の方程式
・ 複数項目の合計が同じ
・ 計算できる
表の空欄推測では、空欄部分の求め方にいくつか頻出のパターンがあります。問題ごとにパターンを考えるよりも、知っているパターンに当てはまるかどうか確認する方が簡単に解くことができるでしょう。
他の項目と比例しているパターンは、空欄推測の基本です。「来客数と売上」のように、片方が増えればもう片方も増えることが自然な組み合わせでは、比例関係が多くみられます。他の数値の推移から、比例の係数を計算することで空欄が求められます。
また、特定の方程式に則って数値が決められているパターンもあります。この場合、「A×300-B=C」のように、少し変形した比例の式で表すことが可能です。
このパターンでは、「Cの下2桁がBの下2桁と同じ」「Bを足すと丁度いい数値になる」といったヒントが散りばめられています。表全体を見て、こうした関連性に気付けるかがカギになるでしょう。
一方、比例を使わないパターンもあります。縦列や、特定の項目同士の合計が同じという法則は、比例や方程式で求めることができません。「別々の商品の売上」のように、比例関係が生まれにくそうなテーマで用いられやすいパターンです。
さらに、他の項目から計算して求められるパターンも存在します。これは、「商品A、B、Cの購入数と合計金額」のような表で使える法則性です。「AとBを1個ずつ」 「Bを1個だけ」といった2種類の合計の差額から、Aの1個あたりの金額を求めることができます。
表に含まれる数値が、個数を表す1~2桁の数字とそれぞれの合計金額だけである場合、こうした計算問題であることが予想できます。
これらの4パターンを押さえておけば、表の空欄推測を有利に進めることができます。1から法則性を考え出すよりも素早く計算に移れるので、解答時間にも余裕を持たせられるでしょう。


.webp)





.webp)