【SPI 集合｜非言語（数学）】練習問題から対策方法まで一挙公開！

SPIの集合とは？

SPIの集合では、複数の集合に関する情報が与えられ、それをもとに答えを導く問題が出題されます。 具体的にどのようなものなのか、例題と共に見ていきましょう。

【解答・解説】

C.220

図の青い部分を求めたい。 英語だけ話せる人：200 – 50= 150人 日本語だけ話せる人：120 – 50= 70人 したがって、求めるべき人数は150 + 70= 220人

複数の集合(ここでは「日本語を話せる人」と「英語を話せる人」)を視覚的にわかりやすく表したものは「ベン図」と呼ばれます。

集合の問題では、このベン図を使って集合間の関係を考え、答えを導くことが求められます。

そのため、多層的な情報を正しく把握する力が必要となります。

また、ベン図を上手く扱えるかどうかは、集合の問題で高得点を取れるかどうかの分かれ目になります。自在に操れるようになるまで繰り返し演習しましょう。

対策のポイント

上述の通り、集合の問題で高得点を取るカギはベン図です。

ここではベン図を扱う上でのポイントを二つ、ベン図と等式を組み合わせる仕方を一つご紹介します。

ベン図は見やすく

まず一つ目のポイントとして、ベン図は見やすさを重視して描きましょう。

集合の問題では、様々な部分に関して様々な数字が与えられるので、それらの数字をベン図に書き込む必要があります。

その際、ベン図が小さいと書き込み難いだけでなく、図全体がごちゃごちゃしてしまい何が書いてあるのかわからなくなってしまいます。

そうならないために、①ベン図は大きく、②数字は集合の真ん中に書くなどのマイルールを決める、という二点を意識して描いてみましょう。

名前をつける

二つ目に、集合の各部分に名前をつけることも重要です。 例題を用いてご説明します。

【解答・解説】

C.15

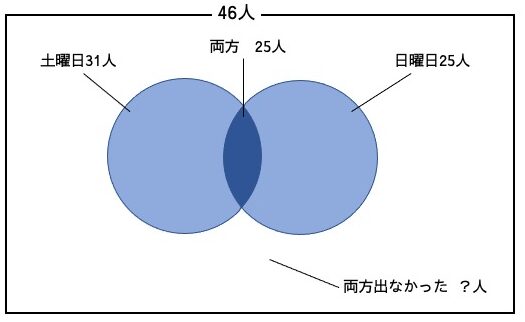
両方の試合に出た人は図の濃い青い部分であり、土曜日の参加者が31人、日曜日の参加者が25人であることから最大で25人である。 このとき、両方の試合に出なかった人の人数も最大になるので、求めるべき人数は、 46 – (31 + 25 – 25 ) = 15 人

この問題では、「土曜日だけ試合に出た人」、「日曜日に試合に出なかった人」、「土曜日と日曜日に試合に出た人」、「どちらにも試合に出なかった人」など、様々な情報が与えられています。

ですが、文のまま解こうとすると、「出なかった」や「だけ」など、結局それがベン図のどこを指しているのかわからなくなることがあります。

これを避けるためにベン図の各部分に名前をつけてみましょう。

例えば、土曜日だけ出た人をA、日曜日だけ出た人をB、両日とも出た人をCと置いてみると、この問題で求めるべきは、AでもBでもCでもない部分であるとすぐにわかります。

このように文字で整理すると考えやすくなります。

等式も有効

最後のポイントは、二つ目のポイントの応用と言えます。

つまり、ベン図の各部分につけた名前を式にすることで、簡単に答えを求めることができるのです。

【解答・解説】

A.9

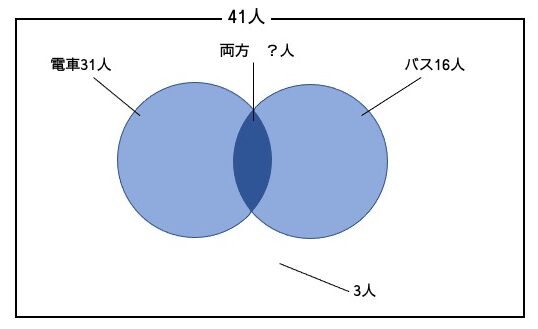求めるべき人数は上図の濃い青い部分。これをxとおく。 よって、31 + 16 – x + 3 = 41 が成り立つので、これを解くとx = 9 したがって電車とバスの両方を使う人は9人。

例えば上の問題で、電車のみの人をA、どちらも使う人をB、バスのみの人をCと名前をつけたとしましょう。

この時、ただベン図を見つめているだけではなかなか答えはわかりません。

ですが、これらの文字と、あらかじめ与えられている数字を組み合わせて式を作ると、難なく答えが求めることができるのです。

これら、ベン図と文字と式の三つを駆使して集合の問題を得点源にしましょう。