【SPI 推論｜非言語（数学）】練習問題から対策方法まで一挙公開！
SPIの推論とは？
SPIの推論の問題では与えられた情報から、正しい選択肢を選ぶことが求められます。
複雑な計算や前提知識は必要ありませんが、基礎的な計算能力と論理的思考力が必要になります。
SPIの問題では1つの問題にかけることができる時間が約1分程度であると言われています。
制限時間内に解答を導き出すことができるように、推論の出題パターンやポイントを把握して受験に臨むようにしましょう。
推論は最頻出単元
推論はSPIで最も出題される単元です。
つまり、推論の問題を解くことができなければSPIで高得点を取ることは難しくなってしまいます。反対に推論の問題を解くことができれば、SPIで高得点を取りライバルに差をつけることができます。
以上のことから、推論は最重要単元であるため徹底的に対策することが必要です。
推論の問題パターン
正誤
正誤を判定する問題では、与えられた情報を正しく読み取り正しい選択肢を選ぶ必要があります。
文章をしっかり読み問題の内容を正しく理解しましょう。
例題
【問題】
X、Y、Zが同じ絵を見てて、次のように発言した。
X この絵には虎が描かれている。
Y この絵には少なくとも虎か龍が描かれている。
Z この絵には龍が描かれている。
全員が本当のことを言っているとは限らない。そこで、以下の推論がなされた。次のうち正しいものを一つ選びなさい。
＜選択肢＞
- Yが正しければXは必ず正しい
- Zが正しければYは必ず正しい
- Xが正しければZは必ず正しい
【解答・解説】
B. Zが正しければYは必ず正しい
Yが正しいとしても、虎が入っていることは分からないため、Xは必ずしも正しくない。
Zが正しいとき、少なくとも龍は入っているため、Yは正しい。
Xが正しいとしても、龍が入っていることは分からないため、Zは必ずしも正しくない。
対戦
与えられた条件から対戦成績を読み取り、正しい選択肢を選ぶ問題です。
対戦表を自分で書いて情報を整理するのが良いでしょう。
例題
【問題】
X、Y、Z、Wの4人がテニスのリーグ戦をおこなった。勝敗について以下のことがわかっている。
Ⅰ YはXだけに負けた。
Ⅱ WはXに勝った
必ず正しいといえる推論はどれか。AからHで1つ選びなさい。ただし、引き分けはないものとする。
ア Xが1勝2敗なら、Wも1勝2敗
イ Zが全敗なら、Xは2勝1敗
ウ Wが1勝2敗なら、Xは2勝1敗
＜選択肢＞
- アだけ
- イだけ
- ウだけ
- アとイ
- アとウ
- イとウ
- アとイとウ
- 正しい推論はないYが正しければXは必ず正しい
【解答・解説】
B. イだけ
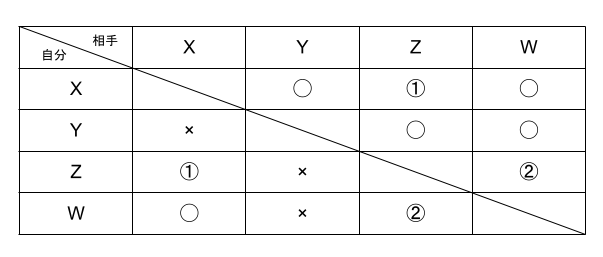
以上の図を参照する。
ア Xが1勝2敗なら、Wも1勝2敗 ←①が×で確定するが、②が確定しない
イ Zが全敗なら、Xは2勝1敗 ←①も②も×で確定する
ウ Wが1勝2敗なら、Xは2勝1敗 ←②が×で確定するが、①が確定しない
従ってイのみ正しい。
割合
推論の割合の問題では、食塩水の濃度や人口密度など対象の割合に関する問題が出題されます。
例題
【問題】
あるラーメン屋の売上について調べたところ、前の月に対して20%ずつ増えている。この時、次の推論について述べたものとして、AからCの中で正しいものを1つ選べ。
・このラーメン屋の売上は、この2ヶ月間で40%増加した
＜選択肢＞
- 正しい
- どちらともいえない
- 誤り
【解答・解説】
C. 誤り
2ヶ月前を100とおくと、
1ヶ月後 100×1.2=120
2ヶ月後 120×1.2=144
と増加していくので、2ヶ月では最初より44%増加したことになる。
整数
整数の問題ではカードの数や人数、数の組み合わせなどを推測する問題が出題されます。
与えられた条件から確実にわかることを整理するようにしましょう。
例題
【問題】
P、Q、Rはそれぞれボールを持っていて、次のことがわかっている。
Ⅰ 3人合わせて8個のボールを持っている。
Ⅱ PとQは同じ個数のボールを持っている。
Ⅲ RはPの2倍のボールを持っている。
このとき、Rは何個のボールを持っているか。
＜選択肢＞
- 1
- 2
- 4
- 5
- 6
【解答・解説】
C. 4
Ⅱ、Ⅲの情報から、P=xとおくと、Q=x 、R=2xとなる。
さらにⅠの情報よりボールの個数の総和が8個だから、x + x +2x = 8 より、x=2であり、Rの持っている個数は4個。
平均
平均の問題では平均の考え方を使って正しく推測する選択肢を選ぶ必要があります。
合計を個数で割ったものが平均であることがわかっていれば、応用して問題を解くことができます。
与えられた情報を冷静に整理するようにしましょう。
例題
【問題】
P、Q、R、Sの4人が100点満点のカラオケの採点をしたところ、次の結果になった。
Ⅰ 4人の平均点は60点だった。
Ⅱ QとRの平均点は50点であった。
Ⅲ SはPよりも10点高かった。
このとき、必ず正しいといえる推論の組み合わせはどれか。
＜選択肢＞
- アだけ
- イだけ
- ウだけ
- アとイ
- アとウ
- イとウ
- アとイとウ
- 正しい推論はない。
【解答・解説】
C. ウだけ
ア: SとQの点数の上下関係は分からないので、必ずしも正しいとは限らない。
イ: 少なくともQとRの点数の上下関係は分からないので、必ずしも正しいとは限らない。
ウ: 4人の合計点は60×4＝240点。QとRの合計点は50×2＝100点。よって、PとSの合計点は240－100=140点。よって、Sは、(140＋10)÷2 = 75点。QとRの平均点は50点なので少なくともどちらかは75点以下である。よって、これは正しい。
位置関係
位置関係を推論する問題では、建物や部屋、座席など位置関係や配置を推測する問題が出題されます。
情報から読み取れることをメモして整理すると良いでしょう。
例題
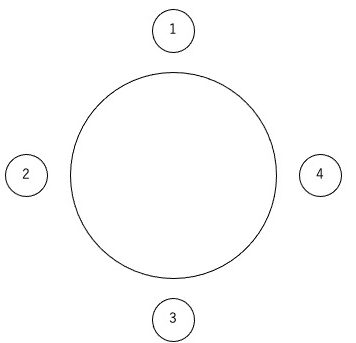
【問題】
X 、Y、Zの3人が、円形に並んだ４つの席のいずれかに座っている。各自の座り方について、次のことが分かっている。
Ⅰ XとYは隣り合っていた。
Ⅱ 数字の2番の席は空席だった。
Zが座った可能性のある席の番号はいくつか。
＜選択肢＞
- １
- ３
- ４
- １か３
- １か４
- ３か４
順序
順序の問題では、順位や順番、並び方に関する問題が出題されます。
与えられた情報からわかることをメモして整理しましょう。
条件からある程度候補を絞ることができたら、パターンを全て書き出して考えても良いでしょう。
例題
【問題】
ＰＱＲＳの4人チームで毎年恒例のサッカーの総当たり戦が行われた。
順位に関して次のことが分かっている。なお、同じ順位のチームはない。
Ⅰ Ｐは昨年より順位が3つ下だった。
Ⅱ Ｑは今年と昨年で順位が変わらなかった。
Ⅲ Ｒは今年2位であった。
今年の順位を左が上位として並べたとき、ただしいものを選べ。
＜選択肢＞
- SRPQ
- SRQP
- PRSQ
- RPQS
【解答・解説】
B. SRQP
Ⅰ、Ⅲより、次のことが分かる。
昨年 Ｐ〇〇〇 今年 〇Ｒ〇Ｐ
これとⅡより、次のことが分かる。
昨年 Ｐ〇Ｑ〇 今年 〇ＲＱＰ
よって、今年はＳＲＱＰ
対策のポイント
SPIで高得点を取るには推論を対策することが欠かせません。
以下では、推論対策のポイントをご紹介します。
問題文を正しく理解する
対策のポイントの1つ目は、「問題文を正しく理解する」ことです。
推論の問題は他の非言語（数学）の問題と違い、読む文章量が多いことが特徴です。
そのため、計算能力だけではなく文章を正確に理解する言語的な能力も問題を解く上で必要となります。
制限時間を意識しながらも、重要な条件を読み間違えることがないように気をつけましょう。
メモをとる
対策のポイントの2つ目は、「メモを取る」ことです。
推論の問題では、与えられた情報を正しく読み取る力が求められます。
その際、文章や条件からわかることを簡単にメモすると情報の整理がしやすくなります。
以下は、メモを取る際のコツです。
情報を図式化する
1つ目のコツは情報を図式化することです。
情報を図式化すると、視覚的に情報を整理することができます。
特に「順序」や「対戦」、「位置関係」の問題では図や表にして情報を整理すると、情報の整理がしやすくなります。
メモのルールを決めておく
2つ目のコツはあらかじめメモのルールを決めておくということです。
メモを取る際は、記号や符号を用いて簡単にメモすることが重要ですが、自分なりのルールを決めておかないとメモはしたが、自分でもメモの意味がわからないということになってしまいます。
あらかじめ、メモの取り方を決めて問題を解くようにしましょう。
重要な条件を見極める
対策のポイントの3つ目は、重要な条件を見極めるということです。
推論の問題では、条件から確実にわかることを正しく判断する必要があります。
制限時間内に効率よく推論するためには、より選択肢を狭め、限定することができる条件を見極めることが必要です。
文章の中に、重要な条件が紛れていることもあるため注意して文章を読むようにしましょう。
推論
問題一覧
1
問題1-1（正誤）
2
問題1-2（正誤）
3
問題1-2（正誤）
4
問題1-3（正誤）
5
問題1-5（正誤）
6
問題1-6（正誤）
7
問題2-1（対戦）
8
問題2-2（対戦）
9
問題2-3（対戦）
10
問題2-4（対戦）
11
問題3-1（割合）
12
問題3-2（割合）
13
問題3-3（割合）
14
問題3-4（割合）
15
問題3-5（割合）
16
問題3-6（割合）
17
問題4-1（整数）
18
問題4-2（整数）
19
問題4-3（整数）
20
問題4-4（整数）
21
問題4-5（整数）
22
問題4-6（整数）
23
問題4-7（整数）
24
問題4-8（整数）
25
問題4-9（整数）
26
問題4-10（整数）
27
問題4-11（整数）
28
問題4-12（整数）
29
問題4-13（整数）
30
問題4-14（整数）
31
問題4-15（整数）
32
問題4-16（整数）
33
問題4-17（整数）
34
問題4-18（整数）
35
問題4-19（整数）
36
問題4-20（整数）
37
問題4-21（整数）
38
問題4-22（整数）
39
問題4-23（整数）
40
問題4-24（整数）
41
問題4-25（整数）
42
問題4-26（整数）
43
問題4-27（整数）
44
問題4-28（整数）
45
問題4-29（整数）
46
問題4-30（整数）
47
問題5-1（平均）
48
問題5-2（平均）
49
問題5-3（平均）
50
問題5-4（平均）
51
問題5-5（平均）
52
問題5-6（平均）
53
問題5-7（平均）
54
問題5-8（平均）
55
問題5-9（平均）
56
問題5-10（平均）
57
問題5-11（平均）
58
問題5-12（平均）
59
問題6-1（位置関係）
60
問題6-2（位置関係）
61
問題6-3（位置関係）
62
問題6-4（位置関係）
63
問題6-5（位置関係）
64
問題6-5-2（位置関係）
65
問題6-6（位置関係）
66
問題6-7（位置関係）
67
問題6-7（位置関係）
68
問題6-8（位置関係）
69
問題6-9（位置関係）
70
問題6-10（位置関係）
71
問題6-11（位置関係）
72
問題6-12（位置関係）
73
問題6-12（位置関係）
74
問題7-1（順序）
75
問題7-2（順序）
76
問題7-3（順序）
77
問題7-4（順序）
78
問題7-4（順序）
79
問題7-5（順序）
80
問題7-6（順序）
81
問題7-7（順序）
82
問題7-8（順序）
83
問題7-9（順序）
84
問題7-10（順序）
適性検査SPI3対応！言語・非言語対応のSPI対策アプリ！
問題クリエイター
Ryosuke
2002年生まれ。早稲田大学の3年生。現在、24卒として就職活動しながらSPIの研究を行い、 『SPI対策問題集』の立ち上げを担当。同じ大学の友人らと協力して問題の制作や解説記事の作成を行う。 非言語科目を得意としており、特に推論の問題には大きな自信を持っている。
監修者
gen
1990年生まれ。大学卒業後、東証一部上場のメーカーに入社。その後サイバーエージェントにて広告代理事業に従事。 現在はサイバーエージェントで培ったWEBマーケの知見を活かしつつ、CareerMineの責任者として就活生に役立つ情報を発信している。 また自身の経験を活かし、学生への就職アドバイスを行っている。延べ1,000人以上の学生と面談を行い、さまざまな企業への内定に導いている。
>メッセージを読む
人気記事
