【SPI非言語対策ガイド】出題形式や対策方法まで例題付きで徹底解説！

SPIの非言語分野とは？

SPIとは、リクルートマネジメントソリューションズが提供する「総合適性検査（Synthetic Personality Inventory）」のことです。

 

このSPIは「性格検査」と「能力検査」の2つから構成されており、「非言語分野」は能力検査におけるテスト科目の1つです。

能力検査で出題される科目は大きく分けて「言語（国語問題）」「非言語（論理・数学問題」「英語」の3つになります。

 

この記事では「非言語分野」について、特徴や対策方法、出題形式について紹介しています。

SPI非言語の特徴

非言語分野では、いわゆる「数学の問題」が出題されます。「四則演算」を用いた基本的な計算から、図表などから情報を読み取る問題、最も難しいといわれている「推論」などの問題を通じて、数的処理能力や論理的思考力が見られています。

 

主に出題される分野は下記9つになります。

 

SPIの非言語問題は、中学校で習う数学が試験範囲とされているため、決して難易度が高いわけではありません。しかし、公式や考え方を理解していないと解けない問題が多いため、対策せずに臨むのは避けましょう。

 

また非言語では幅広い分野から出題されるため、高得点を獲るためには全ての分野を抜かりなく勉強する必要があります。

 

そのため、一夜漬けや直前での対策で高得点を獲るのは難しいといえるでしょう。早い段階からSPI対策に取り組み、苦手分野の克服に努めるのが高得点を得るためのポイントとなります。

 

受検する方法によっても、出題数や問題を解く時間が異なってきます。

 

	実施時間	言語問題の出題数
テストセンター	言語・非言語あわせて約35分	回答状況によって出題数が変わる
ペーパーテスト	40分 ※言語と非言語は別々に実施	30問
WEBテスティング	言語・非言語あわせて約35分	回答状況によって出題数が変わる

 

SPI非言語問題の特徴は、「回答時間が短く、問題数が多い」こと。先述した通り、問題のレベル自体はそこまで高くないですが、制限時間内に解く問題数が多いため、正確さと時間のバランスが大事になります。

 

正確に解けるような対策と平行して、時間を意識し素早く解くための特訓が必要になります。

 

またテストセンターとペーパーテストでは、同じ設定で2〜4問の問いが続く「組問題」が出題されます。

 

設定を理解することで早く解くことができますが、実際には設定を理解するのに時間がかかってしまうため、結果として1問にかけられる時間がどんどん短くなってしまう傾向にあります。

 

「組問題」に慣れておくことも、非言語での正答率をあげる対策の1つといえるでしょう。

 

基本的には30分程度の時間で30問前後の問題が出題される傾向にあるため、1問にかけられる時間は1分程度です。ゆっくり考えながら解く時間の余裕はありません。

 

難しい問題やわからない問題が出てきた際には、すぐに次の問題へと進み、確実に解ける問題に注力するのが良いでしょう。

 SPI非言語の対策方法

出題範囲の広いSPIの非言語で高得点を取るためには、出題される問題の形式を理解し、全ての分野の問題に取り組んでおくのがベストでしょう。

 

幅広い分野の対策が必要となるので、言語対策よりも非言語対策の方が時間がかかります。

 

特に高い頻度で出題される「推論」は、理解した上で問題に慣れるまで時間がかかるので、一番最初に対策に取り組むのがおすすめです。

 

推論は、「テストセンター」「ペーパーテスト」「WEBテストライティング」の全ての方式で最も頻出される分野です。

 

「推論」を制することが、非言語分野で高得点を得るための近道といえるでしょう。推論は苦手とする学生も多く、難しい、時間が足りない、解けないというネガティブな声が多く聞かれます。

 

推論の解き方を理解したら、多くの問題を解き、苦手意識を克服しておきましょう。推論問題を多く扱っている対策本や推論に特化して解説しているWebサイト、単元別に繰り返し学習できるアプリなどを活用するのがおすすめです。

 

ここではSPIの非言語で得点アップをはかるためにやるべきことを2つ紹介します。

公式・数式・解法パターンを暗記する

非言語分野においては公式・数式を知らないと解けない問題が大半です。まずは、必要最低限の公式・数式を徹底して暗記しましょう。

 

次に練習問題を多く解き、出題パターンとその際の解法パターンを確認していきます。同じ分野の設問でも求める内容によって使用する公式が異なります。出題パターンを掴むことで、それに対する公式や数式がすぐに出てくるようになります。

 

SPIは短時間で多くの問題に解答しなくてはなりません。そのためには少しでも悩む時間を減らすこと、すなわち出題パターンにあった解法パターンがパッと出てくることが望ましいです。

 

丸々暗記するのではなく、応用にも対応できるように解き方を理解し進めていきます。そのためには多くの問題に触れ、苦手分野を1つでも減らすよう対策していきましょう。

わからない問題はすぐに解説を確認する

SPI対策では、とにかく多くの問題をこなすことが大切になります。そのため、じっくり考え込んで解き方を学ぶよりも、わからない問題はすぐに解説を確認し、理解することを繰り返す方が効率良く勉強することができます。

 

また多くの問題集や過去問を片っ端から解くのではなく、1〜2冊の問題集（対策本）を何度も繰り返し、完璧に解けるようにすることが高得点を得るための近道となります。

非言語分野で出題される問題形式と解き方のコツ

推論

推論とは、与えられた情報をもとに正しい順番や内訳を導き出すことです。推論には数種類の出題パターンがあり、その種類に応じた解き方をマスターする必要があります。

 

先述した通り、推論はテストセンター、ペーパーテスト、WEBテスティングの全方式で出題される頻出分野となります。

 

推論は他の問題よりも情報整理に時間がかかるため、出題パターンを把握し、繰り返し解き問題に慣れておくことが大切です。

 

主にテストセンターとペーパーテストで出題される問題のパターンは7つです。

 

順序	与えられた情報から正しい順番を答える問題
密度	与えられた情報から人口密度を算出する問題
発言の正誤	1人もしくは複数の発言から矛盾を見つける問題
対戦	与えられた情報から対戦結果を導き、選択肢の中から正しいものを選ぶ問題
位置	与えられた情報から想定される位置関係を洗い出し、選択肢の中から正しいものを選ぶ問題
平均	平均から個々の値を算出する問題
内訳	与えられた情報から何が何個あるのか、どこに何人いるのかなどの内訳を答える問題

 

この他にも、設問に対して当てはまるもの全てを選ぶ問題や、条件を使って数値を算出する問題などがあります。

 

受検形式によって、出題される問題の傾向が若干変わることがありますが、まずは上記の7つのパターンを把握し、それを算出するための数式や解き方をしっかりと押さえておきましょう。

 

例えば、平均を出す数式は「平均＝合計÷個数」、増加率など％を用いる場合「10%増加＝×1.1」など、それぞれの解答を導くために必要な数式や公式は暗記しなければなりません。

 

また情報の整理の仕方や表を用いて解く解き方など、パターンによって導き方が異なるので全分野を網羅するためには時間が必要になります。

 

推論を解くための大きなポイントは、「文章を記号や図表を使って整理すること」「全ての事象（場合）を書き出すこと」の2点です。

 

早く回答に導くコツは問題を読みながら記号化、図化すること。そしてミスを防ぐためには、考えられる全ての事象を書き出し、選択に誤りがないかを確認することです。

 

推論を攻略するには、とにかく多くの問題を解き「問題パターンに慣れる」ことが重要です。

問題のパターンを覚えることができれば、問い方や数字が変化したとしても問題が解けるようになります。スラスラと解き方が出てくるようになるまで、繰り返し問題を解きましょう。

表の読み取り

図表の数値を読み取って計算する問題です。推論同様、テストセンター、ペーパーテスト、WEBテスティングの全方式で高い頻度で出題される分野になります。

 

主に出題される表と問題は下記です。

 

数量の表	数量や割合を求める問題
割合（％）の表	数量や割合を求める問題
2つの表	2つの表から数量や割合を求める問題
得点範囲の表	平均点や人数を求める問題

参考：’23 これが本当のSPI3だ！

 

図表の読み取り問題を解くときのポイントは3つです。

 

 

増加率、減少率は、どれくらい数値・値が増えたのか、減ったのかを%で算出します。そのため、％を使った計算にミスがないよう、解き方や計算方法を見直しておきましょう。

 

また得点範囲の問題では、「最小値と最大値を出すこと」が重要なポイントになります。最小最大値を出した上で解答に結びつく問題が多いので、チェックしておきましょう。

集合

調査結果から、1つの項目に該当する人数、もしくは複数の項目に該当する人数などを導き出す問題です。

 

集合問題は、図を書いて情報を整理するのが確実に解く方法になります。図の書き方には2種類あり、「ベン図」と「カルノー表」が主に使用されます。

 

 

「ベン図」とは、呼ばれる重なる円やその他の図形を用いて複数の項目の集合間の関係を表します。

一方、「カルノー表」とは、論理式を簡単化するための表です。カルノー表は2つの項目について考える問題では便利ですが、3つ以上の項目を用いる場合はベン図の方が適しています。

 

ベン図が苦手な人はカルノー表で解くこともできますが、3つ以上の項目にも適応するためにできるだけベン図に慣れておくことが好ましいでしょう。

場合の数

何通りの並び方があるのか、何通りの組み合わせがあるのかを導き出す問題です。公式を使って解いていきます。

 

場合の数は「順列」「組み合わせ」と呼ばれることもあり、対策本やサイトによって表記の仕方が異なります。

 

順列と組み合わせの違いは「順番を考慮するかしないか」です。順列は順番に並べること、組み合わせは何通りあるのか選ぶだけになります。どちらを導き出す問題なのかわからないときには、問題文をよく読みましょう。

 

一例ですが、「並べる」や「列」という言葉が出てきたら『順列の公式』、「選ぶ」や「組み合わせ」という言葉が出てきたら、『組み合わせの公式』を使います。

 

順列・組み合わせの問題は「公式を覚える」ことが、必須となります。『順列の公式』『円順列の公式』『組み合わせの公式』この3つは必ず暗記しましょう。

 

また場合の数の問題で高得点を得るためのポイントは、「様々な種類の問題を解くこと」です。順列・組み合わせの問題では、どの問題でどの公式を使うのかを瞬時に判断することが求められます。

 

そこで使用する公式を間違えないためにも、様々な例題を解いて、問題の読解力をあげましょう。

確率

確率の問題では、主に「くじ引き」を用いた問題が出題されます。引いたくじを戻すか、戻さないかで解き方が異なります。他にも「トランプ」や「サイコロ」「コイン」を用いた問題が出題されます。

 

対策本やWebサイトによって呼び方が異なり、「確率」という表記で解説されている場合と「場合の数」として解説している場合があるので、注意しましょう。

 

確率問題を正確に解くポイントは、「公式を覚えること」です。どの単元にもいえることですが、非言語の問題は基本的な公式や数式を押さえていなければ解くことができません。

 

確率問題では下記5つの公式が必須となります。

 

 

苦手とする人が多い確率問題ですが、全方式で高い頻度で出題される分野になります。出題頻度が高いということは、完璧に解けるように対策しておくことで、確実に点数を取れる問題であるということです。

 

確率問題は、公式と解法パターンを覚え、対策を行いましょう。

金額計算

金額計算の問題は大きく分けて「割引」と「損益算」の2つに分けることができます。

割引

人数や時間によって割引率が異なるときの代金や総額を求める問題です。

 

割引問題で主に使用される公式は2つです。

 

問題中では、割引される人とされない人が混ざっていたり、料金が平均額で提示されていたりします。問題を解くときには、割引される人とされない人を分けて考えることで正解に辿り着くことができます。

 

この他にも、まとめ買いでの割引率を求めたり、平均額から人数を求める問題など、さまざまな角度から割引について問われる設問が出ます。

損益算

品物を仕入れて販売したときの損益を計算する問題です。問題文から「仕入れ値」「定価」「売価」などの数値を割り出し、整理し解いていきます。

 

損益算の難易度はあまり高くないのですが、損益算を苦手としている人はそもそも用語をしっかりと理解していないことが多いです。

 

公式はもちろんですが、まず損益算の基礎となる用語7つを理解しましょう。

 

原価	商品を仕入れた値段
利益	原価に上乗せした分の金額　＝儲けの金額
定価	原価に利益を上乗せした合計金額　＝割引き無しの売値
割引額	定価から減額した額
売値	実際に消費者に販売される値段 ※割引きをせずに販売する場合は「定価」が売値となる
利益率	※何に対しての利益なのかを明確にする必要あり 一言で利益率といっても何通りかあり「何に対しての利益なのか」によって、求め方が変わる 損益算の場合は『原価に原価の何％を利益として上乗せたか？』という意味で使われることが多い
割引率	定価から差し引く割引額の割合　＝割引額は定価の何％なのか

 

要注意なのは、「利益率」と「割引率」です。割合が絡んでくることで問題が複雑に見えますが、数値が何を表しているかを明確にすることが大切です。

 

問題文のままだと何を求めるのかがわかりにくいので、定価や売価、割引率などの数値を取り出し、1つずつ数式化していくことで答えが出ます。

分担計算

分担計算問題は大きく分けて「分割払い」と「仕事算」の2つに分けることができます。

分割払い

分割払い問題とは、商品を分割するときに、現時点でどれだけ支払っているかを求める問題です。

 

考え方としては「分割払い1回当たりの金額は、支払総額の何分の何か？」というのが基本となります。全体を1（支払い総額を1）としたときの割合を考える問題です。

 

総額に対する割合だけではなく、手数料がかかるときの支払額の計算や利子が付いた場合の問題などが出題されます。

 

割合は分数で提示されることがほとんどなので、分数の問題と言い換えることができるでしょう。

仕事算

仕事算とは、複数人で仕事をする場合にかかる時間を求める問題です。主に「公約数と公倍数」「分数」「割合と比」を使って解きます。

 

どれも基礎を押さえておけば問題なく解ける問題です。分数の計算や割合の計算に自信のない人は、もう一度振り返り、基礎をしっかりと固めておきましょう。

速度算

速度算とは、平均速度や追い越し・追いつくのにかかる時間を求める問題です。

 

「速さ」「距離」「時間」の3つの関係を理解しておくだけで解ける問題なので、比較的簡単だといえるでしょう。万が一、公式を忘れてしまったとしても、3つの関係性を理解し、公式を1つ覚えていれば他を導き出すことができます。

 

ただし注意しなくてはならないのは、「単位」です。時間が『分』で表されているときは、『時』に直してから式に当てはめなければなりません。問題をよく読み、正確に解きましょう。

割合

全体のうち、Aの割合は何％かということを計算する問題です。SPIにおける割合と比率の問題は決して難しくありません。

 

掛け算や割り算、足し算、引き算さえできれば解ける問題が多いので、繰り返し問題を解き、出題パターンを把握しておきましょう。

 

問題が文章で説明されるため、状況が掴みづらいのが特徴です。文章を正確に読み取ることがコツです。どのような関係なのか、関係性を図にすると解きやすくなります。

実際に出題された非言語問題

例題｜推論

【問題】

X、Y、Zが同じ絵を見てて、次のように発言した。

 

X.　この絵には虎が描かれている。

Y.　この絵には少なくとも虎か龍が描かれている。

Z.　この絵には龍が描かれている。

 

全員が本当のことを言っているとは限らない。そこで、以下の推論がなされた。次のうち正しいものを一つ選びなさい。

 

【選択肢】

A.　Yが正しければXは必ず正しい

B.　 Zが正しければYは必ず正しい

C.　 Xが正しければZは必ず正しい

 

＞＞解答・解説はこちら

【推論】の問題一覧

例題｜表の読み取り

【問題】

ある小学校の２年生が国語、算数、英語の３教科の試験を受けた。

男子学生の３教科の平均点はいくつか。（必要な時は、最後に小数点以下第２位を四捨五入すること）

 

 

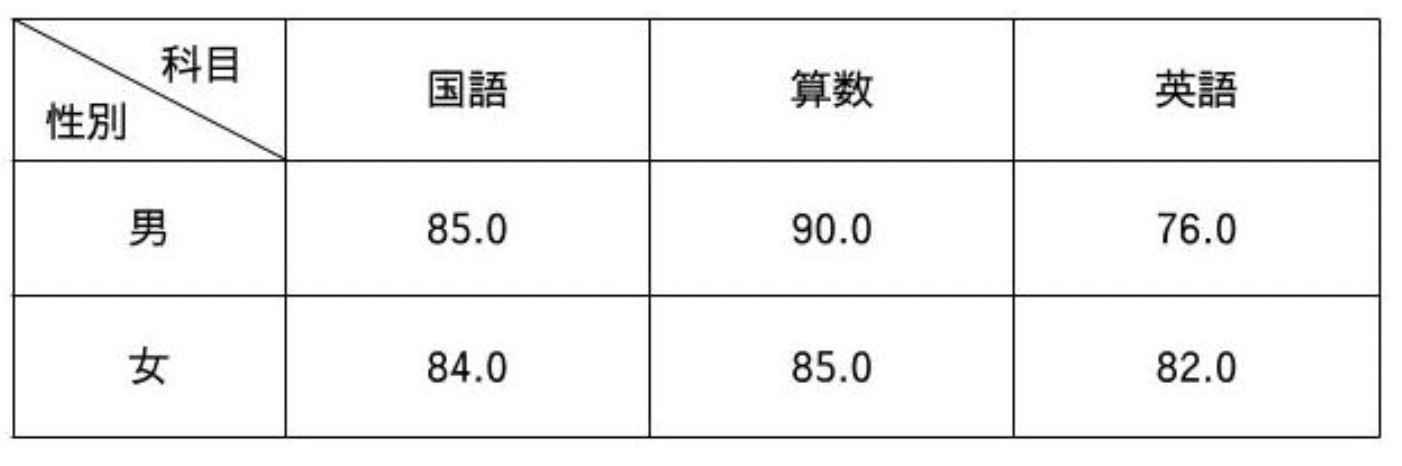
【選択肢】

A.　80.5

B.　83.3

C.　83.7

D.　86.6

E.　90.0

 

＞＞解答・解説はこちら

【表の読み取り】の問題一覧

例題｜集合

【問題】

大学に所属する留学生300人に調査を行ったところ、英語が話せる人が200人、日本語が話せる人が120人いた。この中から、どちらかの言語しか話せない人の人数を調べたい。

 

英語と日本語両方とも話せる人が50人いたとすると、英語と日本語のうちどちらか片方だけ話せる人は何人か。

 

【選択肢】

A.　170

B.　200

C.　220

D.　270

E.　320

 

＞＞解答・解説はこちら

【集合】の問題一覧

例題｜金額計算（料金の割引）

【問題】

あるネットカフェでは2時間以上利用すると料金が最初から1時間は5%、2・3時間目は10％、4時間目以降は20%引きとなる。

1時間1000円の部屋を7時間利用する時、利用料金は合計いくらか。

 

 【選択肢】

A.　 5600円

B.　 5350円　

C.　 5550円

D.　 5950円

 

＞＞解答・解説はこちら

【金額計算】の問題一覧

例題｜金額計算（損益算）

【問題】

原価100円の商品を200個仕入れた。50個を1割引で売ったが、売れ行きが良くなかったので残り150個を2割引で売ったら、利益が合計13000円になった。

定価はいくらだったか。

 

【選択肢】

A.　 150円

B.　200円

C.　220円

D.　300円

 

＞＞解答・解説はこちら

【金額計算】の問題一覧

例題｜分担計算

【問題】

ある書類の処理を全て終わらせるのに，Xは6日間、Yは10日間かかる。この処理をXとYの2人で行う場合、全て終わらせるまでに何日かかるか。

なお2人で処理する場合も時間あたりの処理量は変わらない。

 

【選択肢】

A.　 3日

B.　4日

C.　7日

D.　8日

 

＞＞解答・解説はこちら

【分担計算】の問題一覧

例題｜速度算

【問題】

往路は6km/時の速さでS駅からT駅まで移動し、T駅で2時間買い物をした。復路は10km/時の速さでT駅からS駅まで移動した。すると買い物時間も含めて往復に全部で4時間かかった。往復の移動平均時速を求めよ。

ただし、買い物時間は含めない。また、必要に応じて、最後の結果の小数点第3位以下を四捨五入すること。

 

【選択肢】

A.　6.0km/時

B.　6.5km/時

C.　7.0km/時

D.　7.5km/時

 

＞＞解答・解説はこちら

【速度算】の問題一覧

割合

【問題】

映画館Tではチケット料金を30%値上げした。すると販売枚数が20%減少したが、全体として売上は上がった。売上高は何%増加したか求めよ。

ただし、必要に応じて小数点第二位以下を四捨五入せよ。

 

【選択肢】

A.　1.0%

B.　2.0%

C.　4.0%

D.　 6.0%

 

＞＞解答・解説はこちら

【割合】の問題一覧