目次
「SPI」とは、総合適性検査（Synthetic Personality Inventory）のことです。
SPIは「性格検査」と「能力検査」の2つで構成されています。
「能力検査」で出題される科目は「言語」「非言語問題」が基本で、企業によっては「英語」が出題される場合もあります。
能力検査の中の非言語分野では、「数学の問題」が出題されます。
「四則演算」を用いた基本的な計算から、図表から情報を読み取る問題、問題文から「必ず正しい」と推論を立てる問題などがあります。
このような非言語問題を通して、数的処理能力や論理的思考力が判断されます。
非言語問題は中学〜高校で習う範囲の問題が出題されるので、問題自体の難易度はそこまで高くありません。
しかし、非言語テストは多くの受検者が苦手としています。理由は、解答時間が短いにも関わらず問題数が多いからです。
制限時間内に解答する問題が多いため、解答の正確さと時間のバランスを上手に取ることが必要になります。
1問にかけられる時間は数十秒〜1分程度と短いため、普段から時間を意識しながら問題を解くことが重要です。
苦手意識を持っている人も多い非言語ですが、高度な数学の知識は必要ないため、練習すれば誰にでも解ける問題ばかりです。
基礎的な公式をしっかりと暗記し、問題ごとの解答パターンに慣れてしまえば高得点を狙えます。
SPIの非言語分野は出題の範囲が幅広く、事前対策だけでも時間がかかります。
数学に苦手意識がある学生は多く、対策を上手く進められないこともあるでしょう。
「中学や高校でずっと数学が苦手だった」という人にとっては、非言語は対策のハードルが高く感じるかもしれません。
しかし、問題の基礎を理解することで、こうした苦手意識はなくすことができます。
問題の解き方などが丁寧に書いてある初心者向けの対策本を使って対策を始めてみましょう。
問題の特徴を把握することで、どのような対策をすべきかが見えてきます。
SPIでは主に「Webテスティング」「テストセンター」「ペーパーテスト」の3つの受検形式があります。
受ける企業によって受検方法が異なるので、対策本のみで勉強をしいきなりWebテストを受けると苦戦してしまう可能性があります。
自分が受検する企業がどのテスト形式を実施しているかを予め確認し、事前に本番を見据えた環境で操作を行っておくのがおすすめです。
無料で受検できるWebテスト模試や、対策本に付属してあるペーパーテスト形式の模試などを活用しましょう。
また、模擬試験を積極的に受けてみるのもおすすめです。
SPI対策模試をはじめとした模擬試験サービスを利用すれば、SPI本番を再現した内容や時間設定で問題に取り組むことができます。
推論とは、問題文で与えられた情報を読み解き、「必ず正しい」と推論できる事柄を選択する問題です。
推論は、様々なパターンからパズルのように当てはめていくような形式です。公式や知識などは必要ありませんが、基礎的な計算能力と論理的思考力が求められます。
推論の問題は、読む文章量が多いことが特徴です。そのため、計算能力だけではなく言語的能力も問題を解くのに重要です。
制限時間を意識して、読み間違いしないように気を付けましょう。
推論で出題される問題は大きく分けて7つあります。
| 順序 | 与えられた情報から正しい順番を答える問題 |
| 密度 | 与えられた情報から人口密度を算出する問題 |
| 発言の正誤 | 1人もしくは複数の発言から矛盾を見つける問題 |
| 対戦 | 与えられた情報から対戦結果を導き、選択肢の中から正しいものを選ぶ問題 |
| 位置 | 与えられた情報から想定される位置関係を洗い出し、選択肢の中から正しいものを選ぶ問題 |
| 平均 | 平均から個々の値を算出する問題 |
| 内訳 | 与えられた情報から何が何個あるのか、どこに何人いるのかなどの内訳を答える問題 |
特に、推論はSPIの非言語で必ず出題される分野です。高得点を狙うには、推論対策を避けて通ることはできません。
推論は難易度は高いですが、問題パターンごとの解き方を覚えることでスムーズに解答できるようになります。
先述した通り、推論には7つの分野が存在し、そのパターンごとに解法や導入までの過程が異なります。
それぞれの解法を知ることで、問題を解くスピードを上げることができるようになります。解法を覚えて問題を解くスピードを早くできるようにしましょう。
場合の数とは、ある事柄の起こりうる場合の総数を導き出す問題です。
「全体のパターン数」から「特定のパターン数」を求めることになるため、問題文をしっかり読み込んで条件を理解する必要があります。
場合の数で求めることになるのは、主に以下の2つです。
求めるものによって一定の解答パターンがあるため、暗記すれば難しい問題ではありません。
逆に、その場で計算方法を考え出そうとしていると、非常に時間がかかってしまう内容になっています。
割合は、2つの項目同士の比率や％を求める問題です。
「何と何を比べているのか」「単位は〇倍か〇％か」といった点を注意深く読み取って計算する必要があります。
「比べる数をもとの数で割る」という基礎的な公式さえ理解していれば難しい問題ではありません。
特定のパターンが起こる確率を求める問題です。場合の数の知識が前提として必要になります。
確率を解くときには、基本的な考え方と想像力を持って考えることが求められます。
確率問題は苦手意識を持つ人も多い分、高得点を取ることができれば他の就活生と差をつけることができます。
確率で出題される問題パターンは主に4つです。
パターンごとに計算方法は異なるため、それぞれの解き方に慣れておきましょう。
公式を丸暗記しても対応できないことが多いので、問題集で実践的な練習をしておく必要があります。
集合とは、複数の要素の集合に関する問いに答える問題です。
集合の問題はベン図（集合を図に表したもの）を上手に扱うことで簡単に解くことができます。
設問から自分でベン図を書き出すことで、問題を理解しながら視覚的に解答することができるようになります
X、Y、Z、Wの4人がテニスのリーグ戦をおこなった。勝敗について以下のことがわかっている。
Ⅰ YはXだけに負けた。
Ⅱ WはXに勝った
必ず正しいといえる推論はどれか。AからHで1つ選びなさい。ただし、引き分けはないものとする。
ア Xが1勝2敗なら、Wも1勝2敗
イ Zが全敗なら、Xは2勝1敗
ウ Wが1勝2敗なら、Xは2勝1敗
＜選択肢＞
【解答・解説】
答え：B
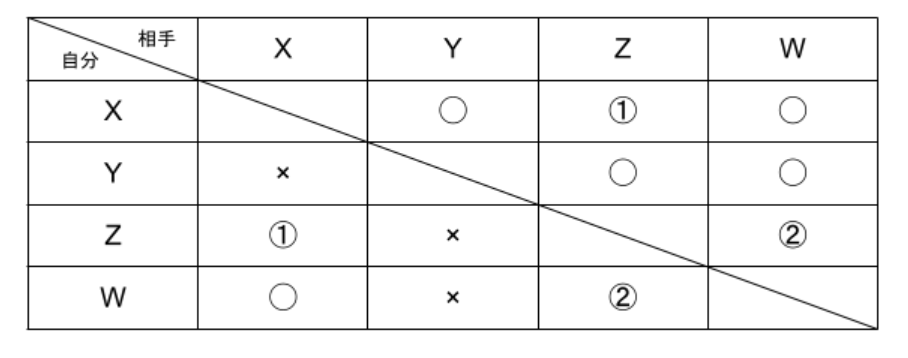
以上の図を参照する。
ア Xが1勝2敗なら、Wも1勝2敗 ←①が×で確定するが、②が確定しない
イ Zが全敗なら、Xは2勝1敗 ←①も②も×で確定する
ウ Wが1勝2敗なら、Xは2勝1敗 ←②が×で確定するが、①が確定しない
従ってイのみ正しい。
ゼミのメンバー10人が旅行に行くことになった。北海道に行く人が3人、沖縄県に行く人が3人、京都府に行く人が4人であるとき、メンバーの行き先の組み合わせは何通りか。
＜選択肢＞
【解答・解説】
答え：D
北海道に行く3人の組み合わせは、10C3 = 120通り。
残りの7人から沖縄県に行く3人の組み合わせは、7C3 = 35通り。
さらに残った4人は自動的に京都行きと来まる。
したがって、メンバーの行き先の組み合わせは、120×35 = 4200通り。
ある劇団の人数は、昨年より40%減って今年は480人になった。男女別では、女性が25%、男性は62.5%昨年より減った。
今年の女性の人数を求めよ。
ただし必要に応じて、小数点第一位以下を四捨五入すること。
＜選択肢＞
【解答・解説】
答え：A
劇団の今年の人数は、昨年の60%なので、昨年の劇団員数は、 480÷0.60=800人 である。昨年の女性の人数を人とおくと、昨年の男性の人数は人である。
男女別では、女性が昨年より25%減って、男性は昨年より62.5%減ったので、今年の女性の人数は人で、今年の男性の人数は人である。
今年の人数は合計480人なので、 が成り立ち、これを解くと人であり、これが昨年の女性の人数である。
従って今年の女性の人数は人である。
球が12個ある。赤色、青色、黄色、緑色の球が3つずつである。この袋の中から、同時にPとQが球を取り出す。1個ずつ取り出すものとする。2人とも赤色の球を取り出す確率を求めよ。
＜選択肢＞
【解答・解説】
答え：B
同時に引く場合、PとQは同じ球を引くことはない。よって、まずPが引いて残った球の中からQが引くとして、両者とも赤色の球を取り出す確率と考えればよく、
大学に所属する留学生300人に調査を行ったところ、英語が話せる人が200人、日本語が話せる人が120人いた。
この中から、どちらかの言語しか話せない人の人数を調べたい。 英語と日本語両方とも話せる人が50人いたとすると、英語と日本語のうちどちらか片方だけ話せる人は何人か。
＜選択肢＞
【解答・解説】
答え：C
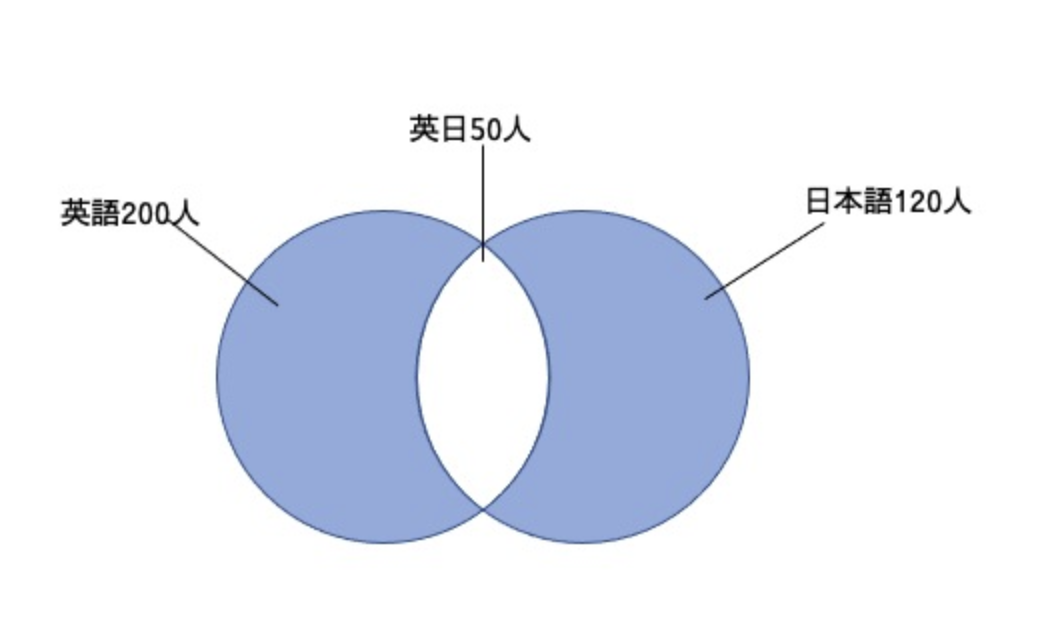
図の青い部分を求めたい。
英語だけ話せる人：200 – 50= 150人
日本語だけ話せる人：120 – 50= 70人
したがって、求めるべき人数は150 + 70= 220人
非言語の問題で高得点を取るためには、1冊の問題集を繰り返し解き、問題と解法をマスターするのがおすすめです。
就活は時間を有効的に使えるかがカギとなります。
何冊もの問題集を解くよりも、1冊分の問題集を完璧にすることで、出題問題の傾向や様々な出題パターンを理解することができます。
問題を見ただけで、解答パターンや公式をすぐに思い出せるレベルまで練習できれば、本番で苦戦することはないでしょう。
書店やインターネットで試し読みをして、使いやすいと思った問題集を選びましょう。
毎年アップデートされる出題傾向に対応するために、なるべく最新版のものを選ぶことをおすすめします。
非言語の問題は、公式や出題パターンを覚えることで問題が早く解けるようになります。
非言語は高校までに習った数学の公式を暗記することで、確率や順列・組み合わせなどの問題を解くことができます。
出題された問題にあてはめるだけで正しく解答できるパターンが多いです。
問題集で計算方法が分からない問題が出てきたときは、必ず解答を見て、公式を覚えるようにしましょう。
SPIでは、効率よく問題を解くことが求められます。解説を熟読して、その場で解けるようになるのが理想的です。
公式を暗記していないと、式を組み立てるのに時間がかかってしまい、大幅なタイムロスに繋がります。
SPIは時間との勝負であり、素早く正確に解くことが求められます。
1問に時間をかけ過ぎると、問題を全て解くことができないため、高得点を狙うことは難しくなってしまいます。
普段から解答時間を計り、スピードを意識しながら練習に取り組むようにしましょう。
時間制限があると、焦ってしまいミスが増えることがあるので、緊張感に慣れておくことも大切です。
非言語では、1問あたり数十秒〜1分程度で解答するのが目安となります。
メモ用紙や電卓も活用し、数秒でも時短できるように取り組みましょう。
出典：Amazon
この問題集は、SPI対策の問題集の中でも人気があり、徹底的に対策できる分かりやすい問題集です。通称「赤本」と呼ばれています。
SPIの受検方式によって問題に違いがありますが、「テストセンター」「ペーパーテスト」「Webテスト」と主要3方式に完全対応しています。
どの問題集を購入するか迷った場合には、この問題集を繰り返し解くことをおすすめします。
出題パターンや苦手問題がわかり、徹底的に対策できます。
出典：Amazon
SPIの基本から学べる対策本です。カラーイラストを交えたわかりやすい解説が特徴的で、苦手意識があっても無理なく学習を続けられます。
また、見開きで左側が知識の解説・右側が練習問題という構成になっており、いちいちページを行き来する必要がありません。
さらに、本番レベルの実践的な模擬テストも付属しているため、対策の仕上げまで1冊でこなせます。
出典：Amazon
この問題集は、難易度が高く問題数が多いのが特徴です。通称「青本」と呼ばれています。
ある程度の学力がある方や、2冊目のSPI対策問題集を探している方におすすめの問題集です。
難易度が高いので、非言語に苦手意識のある方は解説が丁寧な問題集から取り組むのがおすすめです。
ある程度SPIに慣れてから取り組むことでこの問題集を最大限に活かすことができます。
問題数が多いので、様々な問題を解いて力をつけたい就活生は挑戦してみましょう。
苦手意識を持つ人も多いSPIの非言語ですが、実際はほとんどの問題に解答パターンが決まっています。
1冊の問題集に集中して勉強することで、計算や論理的な思考が苦手でも高得点を取ることは十分可能です。
練習問題や模試でとにかく数をこなし、「問題に慣れる」ということを優先して対策を進めていきましょう。
編集者Yuka
監修者gen
